Selection of the Maximum Sampling Speed - The Technical Specification of Acoustic Emission (AE) System
QUESTION:How to select the maximum sampling speed of the AE acquisition system? Is the higher always the better?
This article will discuss the selection of the maximum sampling speed from three aspects: the basic theory of sampling speed, the advantages and disadvantages of high and low sampling speeds, and the application requirements and system matching of the acoustic emission system.
1、Basic Theory
The Sampling Theorem, also known as the Shannon Sampling Theorem or Nyquist Sampling Theorem, states that as long as the sampling rate is greater than or equal to twice the highest frequency of the effective signal, the sampled values will definitely contain all the original signals without missing any signal. In other words, the sampling speed is related to the highest frequency of the signal and should be at least twice to avoid missing any signal.
The principle of sine wave superposition suggests that complex signals can be represented by multiple sine waves of different frequencies and amplitudes (a single frequency and amplitude is a special case). If the highest frequency sine wave component is not missed, the lower frequency components will not be missed either.
Obviously, most application requirements do not just require collecting one value but require collecting the complete information of the entire signal to varying degrees. Theoretically, an infinitely high sampling speed can obtain complete information, i.e., a digital signal with no distortion. This means that the higher the sampling speed, the more complete the digital signal obtained, as illustrated by the solid points in the figure.
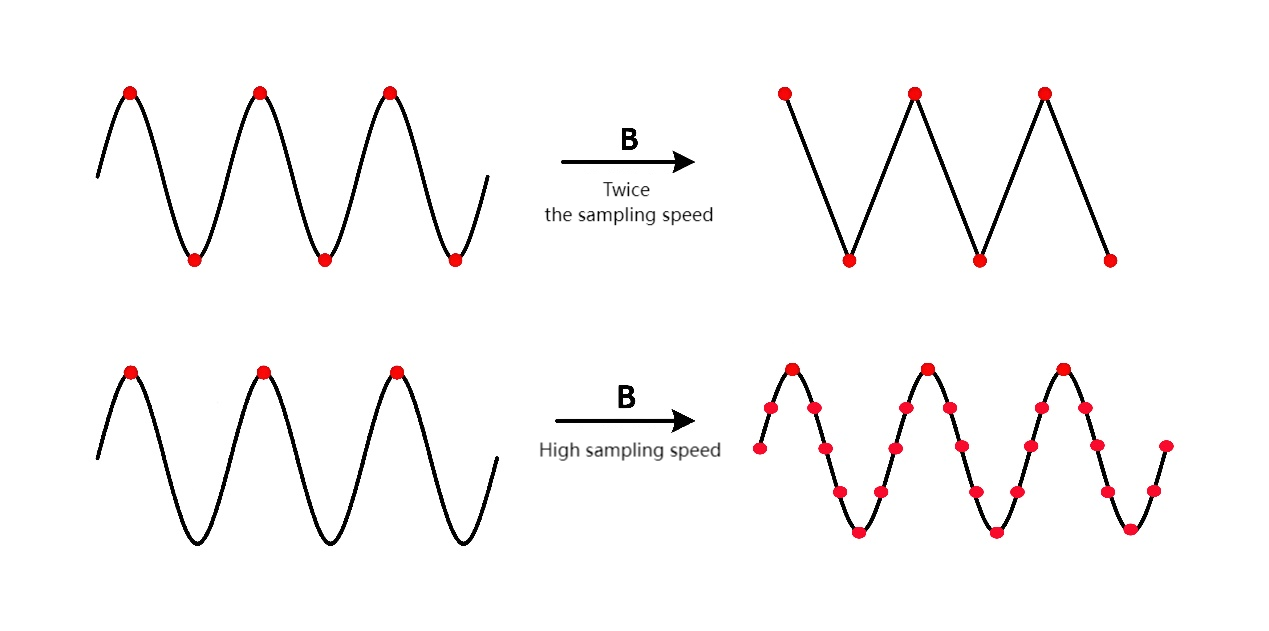
2、Advantages and Disadvantages of High and Low Sampling Speeds
| Sampling Speed | Signal Integrity | Data Volume | Cost |
|---|---|---|---|
| High | Excellent | Large | High |
| Low | Poor | Small | Low |
| Moderate | Good (Meets Application Requirements) | Moderate | Moderate |
Although theoretically, the higher the sampling speed, the more complete the digital signal obtained, considering the actual application cost, it is impossible to achieve infinitely high or even excessively high sampling speeds. Only a reasonable (i.e., meeting application requirements) sampling speed can be selected. For example, a sampling speed of 40 MHz results in 20 times more data than a sampling speed of 2 MHz, and a sampling speed of 10 MHz results in 5 times more data, which will significantly increase the hardware and software burden. If the sampling speed is infinitely high, the increase in data volume and cost will also be infinite. In conclusion, excessively high sampling speeds bring excessively high costs, which is unacceptable. Only by choosing a reasonable moderate sampling speed can it be considered reasonable.
3、Application Requirements and System Matching of Acoustic Emission Systems
How much is a reasonable sampling speed? We can determine a reasonable moderate sampling speed in two steps.
First, determine the highest signal frequency. For example, if the highest signal frequency is known to be 1 MHz, the highest signal frequency cannot exceed the frequency of any hardware or software in the acoustic emission system data flow process. For example, if the sensor bandwidth used is 10 kHz to 1 MHz, the highest signal frequency cannot be greater than 1 MHz, otherwise, the sensor will filter and distort the signal components above 1 MHz. The same principle applies to the circuit frequency bandwidth of each part of the entire data acquisition system. Most actual application requirements (standards and sensor selection) are 100-400 kHz (metal damage), while other applications such as non-metal damage, leakage, collision, etc., have frequency bandwidths lower than 100-400 kHz. Academic research rarely exceeds 1 MHz, and the sensors available in the actual market are not greater than 1 MHz. Therefore, the actual application highest frequency is 400 kHz, and a few academic studies can reach up to 1 MHz.
Then, determine the sampling speed for a sine wave signal with the highest frequency, requiring a few points per half cycle, as shown in the figure. A sampling speed 5 times the highest frequency results in 3 points per half cycle, which in most cases is enough to retain sufficient time-domain waveform and frequency-domain information for application.
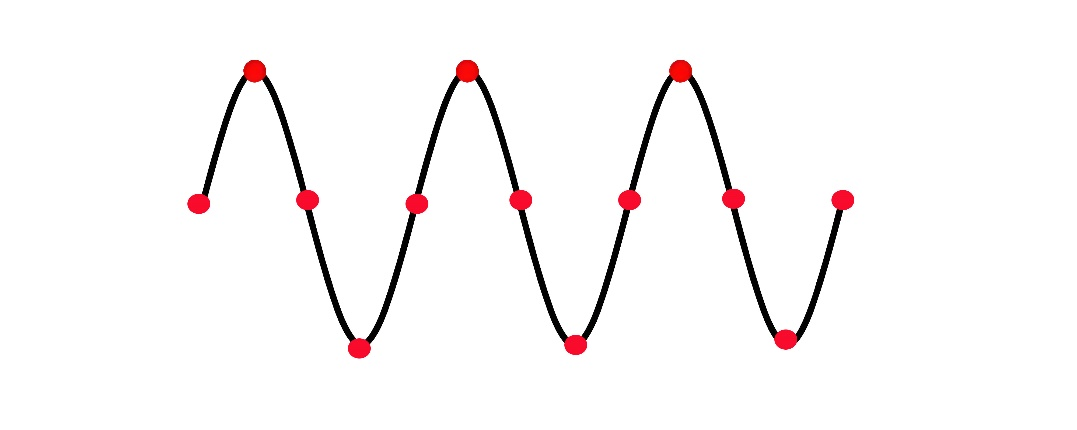
According to the principle of sine wave superposition, the highest frequency component is only a small proportion of the actual signal, and most signal frequency components are lower than the highest frequency. Most low-frequency components will have more than 3 points per half cycle collected at the highest sampling speed, resulting in much less distortion.
The pencil lead break is considered an analog broadband acoustic emission signal including high-frequency signals and is specified as a standard signal by many acoustic emission standards. Figures A and B show the waveforms and FFT diagrams of pencil lead break signals sampled at 2 MHz and 10 MHz, respectively. It can be seen that the main information is retained, and the waveform and FFT differences are not significant. In summary, a sampling speed 5 times the highest signal frequency can meet most practical application needs.
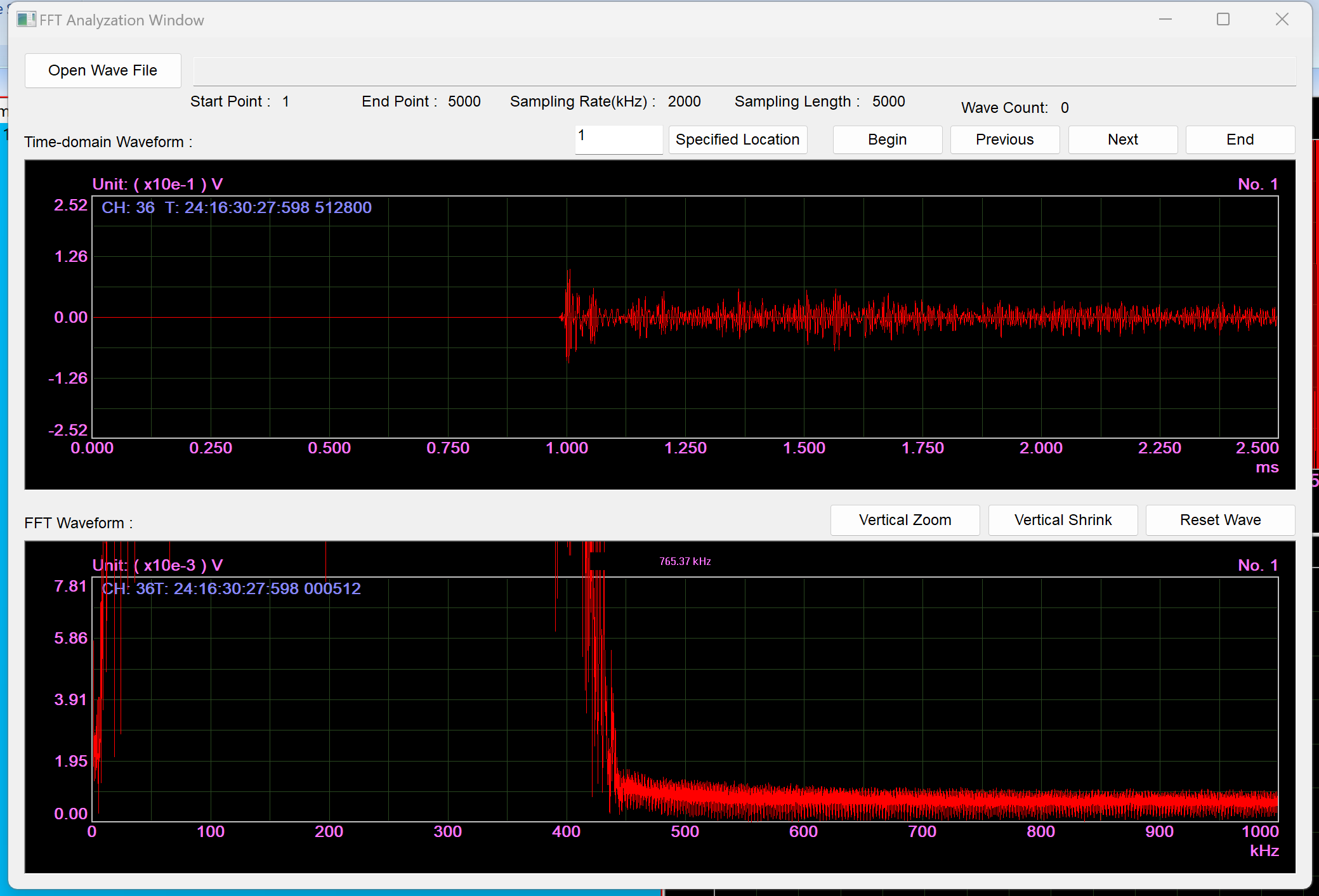
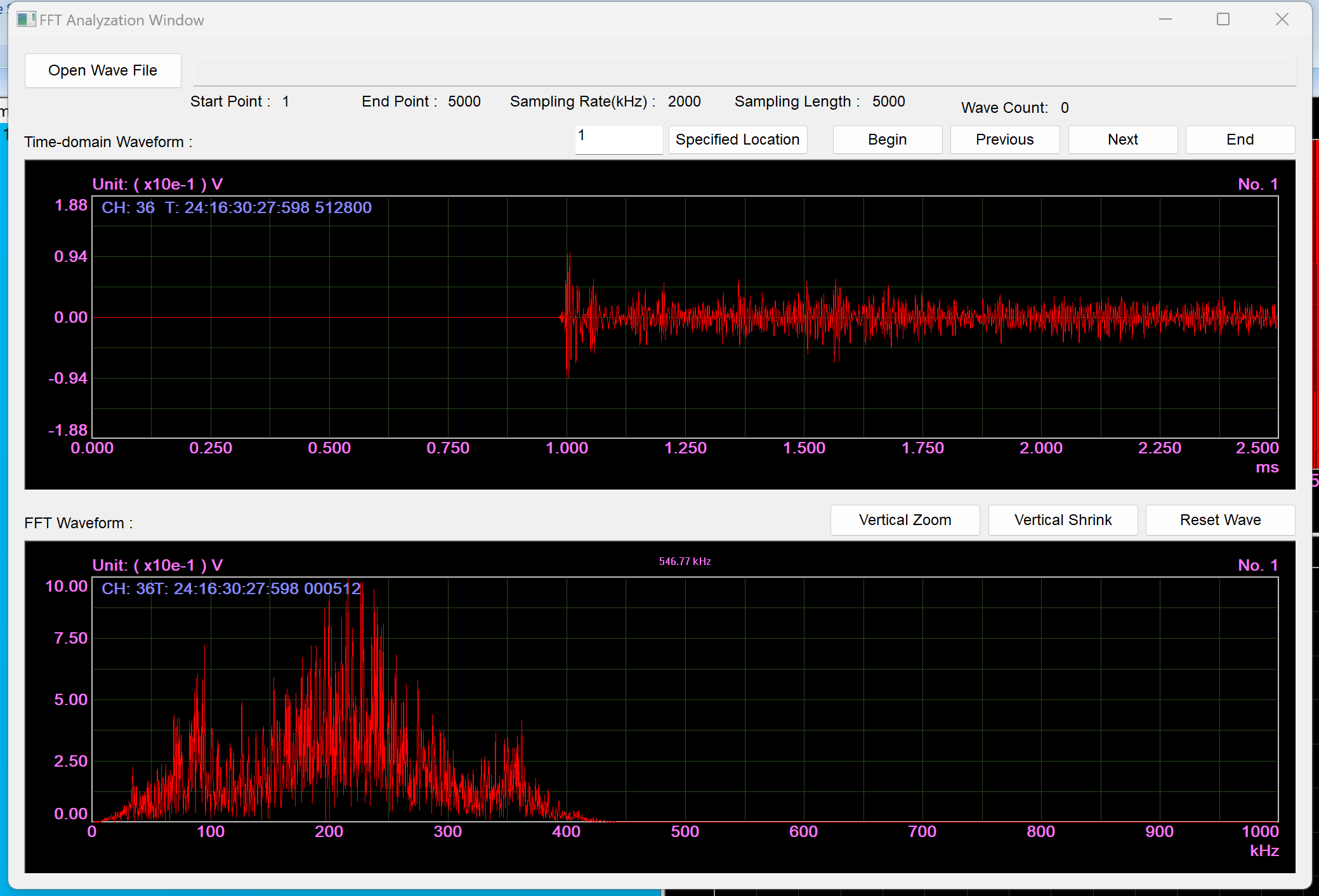
Figure A: Pencil lead break signal, sampling speed 2M, waveform and FFT diagram.
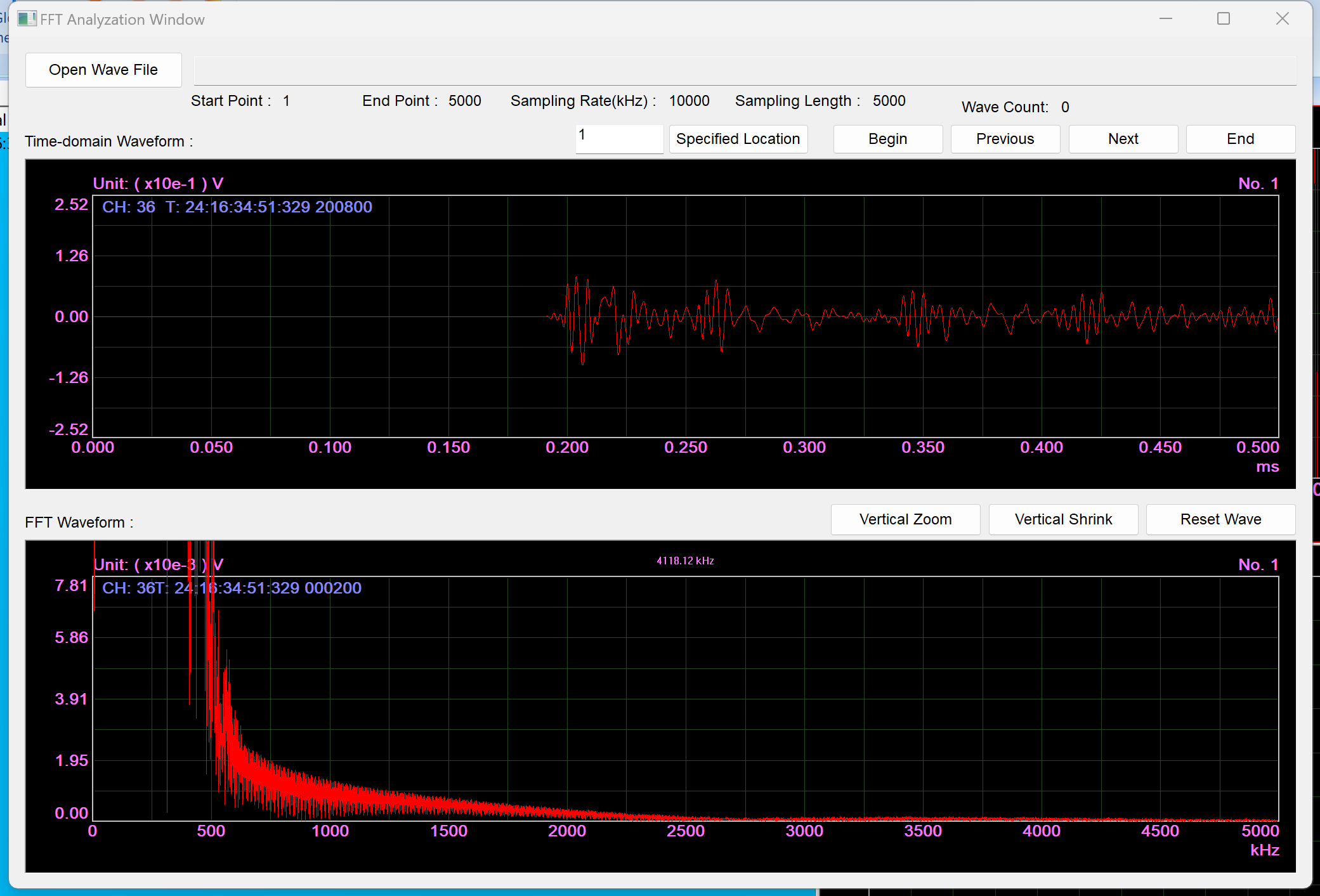
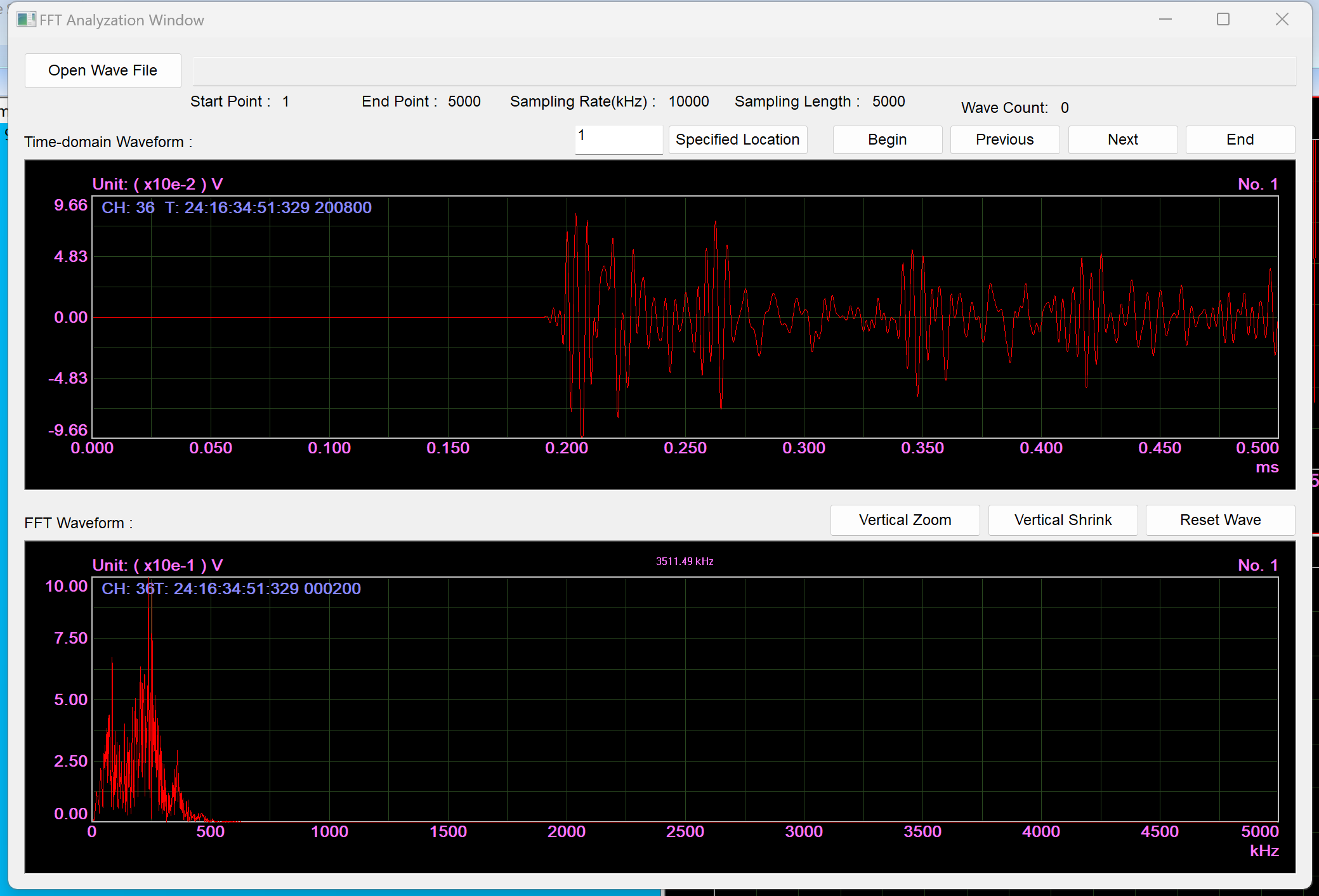
Figure B: Pencil lead break signal, sampling speed 10M, waveform and FFT diagram.
Comparing the vertical coordinates and whether the low frequency is saturated in the two figures indicates that the high-frequency components are minimal and do not affect most practical applications.
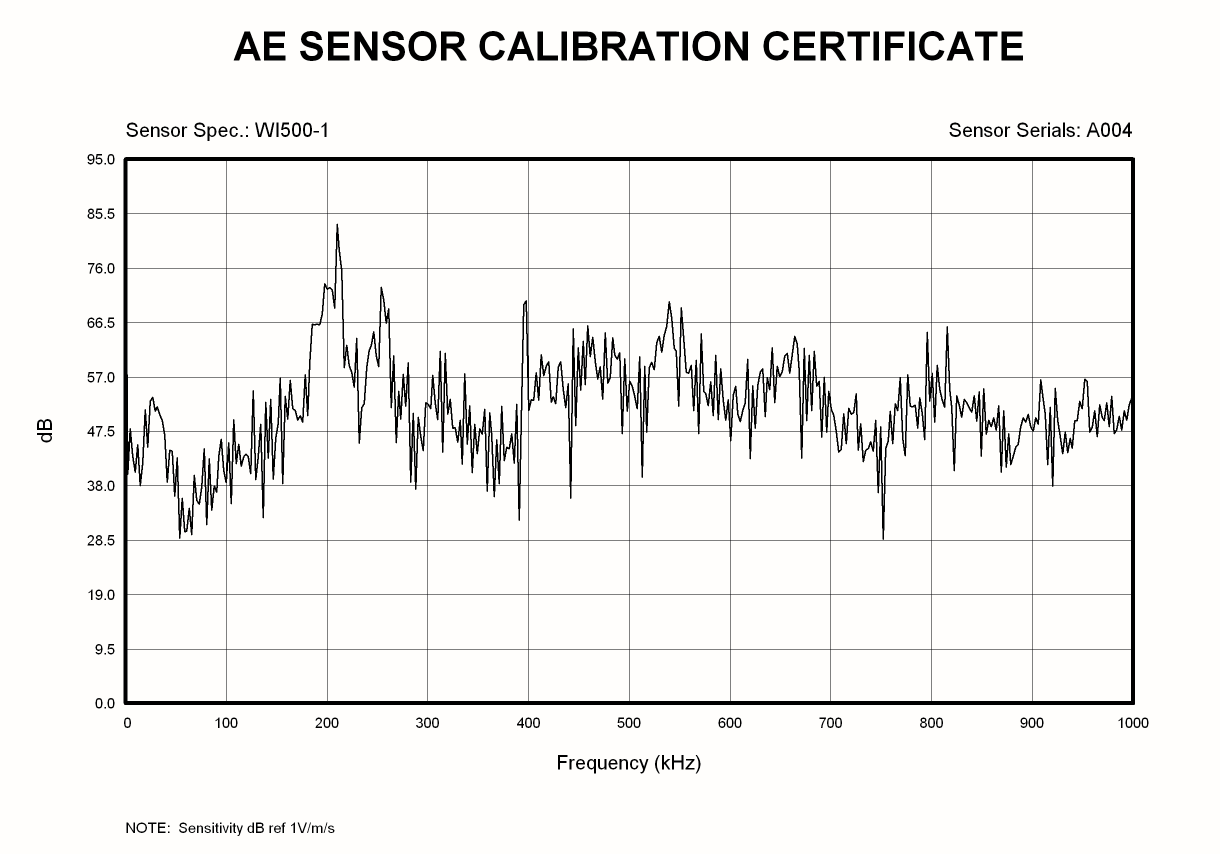
Figure C: Sensor (WI500/1) sensitivity curve.
Data and theoretical calculations show that a maximum sampling speed of 2 MHz meets the data sampling requirements of a maximum signal frequency of 400 kHz, satisfying most acoustic emission application requirements, including metal damage.





